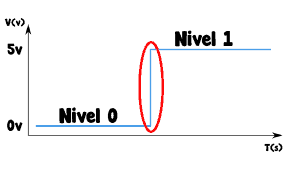
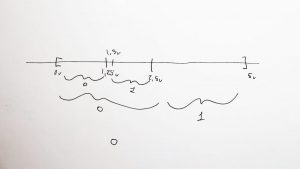
Supón que por algún motivo que discutiremos más adelante necesitas sumar dos señales de tensión. Es decir, tienes una señal de 2 voltios y una de 3.1 voltios y necesitas un circuito que las sume y por tanto te provea a su salida de 5.1 voltios. Esto lo vamos a hacer por medio de un sumador de tensión implementado con un amplificador operacional y unas pocas resistencias.
Podrías pensar, oye pues obtengo una señal de 5.1 voltios directamente ¿no? Supón que ahora la tensión de 3.1 voltios pasa a ser de 4.8 v y por tanto tu nueva salida deberá ser de 6.8 v (2 + 4.8). Con este último supuesto las cosas se empiezan a complicar un poco. Ya no vale la idea de fijar la tensión a 5.1 voltios sino que debemos montar un circuito que sume de verdad. No vale que lo sumemos nosotros.
Amplificador sumador no inversor
Llegada a la conclusión de que necesitamos un circuito sumador para sumar señales de tensión, debemos pensar cómo hacerlo. Si vienes del mundo digital una idea habrá pasado por digitalizar ambas tensiones con un ADC, sumar los valores en algún circuito digital, micro, FPGA o cualquier otro y luego pasar el resultado a un conversor digital a analógico. Siento decepcionarte, pero esto es demasiado sobredimensionado e inadecuado. Tenemos una solución más fácil, usar un amplificador operacional como amplificador sumador no inversor.
El amplificador operacional tiene gran cantidad de posibilidades y es que tenemos muchas configuraciones de amplificador operacional. Una de ellas es la configuración como amplificador sumador no inversor. En ella, el circuito proporciona a la salida la tensión de las entradas sumadas.
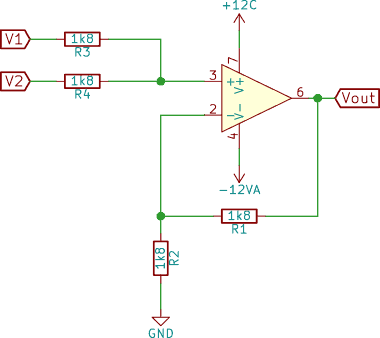
El esquema anterior responde a un sumador de tensión no inversor con el amplificador operacional tl071, aunque podría ser cualquier otro.
El circuito consta de dos entradas V1 y V2 y una salida Vout. Tal cual está, la salida de tensión será la suma.
(1) ![]()
Es decir, que si la entrada V1 es de 2 voltios y la V2 es de 3.1 v, la salida será de 5 v.
Antes he mencionado que es sumador no inversor y esto es debido a que la tensión de salida tiene el mismo signo que la suma. Es decir que si V1 y V2 son positivos, la salida también lo será. En el caso de un amplificador inversor la salida se vería cambiada en signo, sería (-1)·(V1+V2). Y esto es un detalle importante a tener en cuenta.
La clave del funcionamiento de este circuito son las resistencias. Para que se cumplan la ecuación (1) es necesario que todas las resistencias del circuito sean las iguales. En el ejemplo que usaremos, todas las resistencias son de 1k8 Ω, pero si usas otro valor como 10k también funcionará de la misma manera. El uso de resistencias de 1k8 en el ejemplo no tiene otra razón que el simple hecho de que tengo muchas de este valor que tengo que gastar, además en este circuito no es determinante si usamos todas de 10k o de 1k8.
La ecuación del sumador de tensión con amplificador no inversor
Un truco aplicable a la mayoría de circuitos que usan un amplificador operacional con realimentación negativa es hacer un análisis de corrientes de cada una de las entradas del amplificador operacional. En el caso de un amplificador sumador está técnica es perfectamente válida.
Sabemos que la corriente que entra por las entradas inversora y no inversora del Amp.Op. es casi cero. Es tan baja que para hacer los cálculos en un circuito como este podemos considerarlo cero. Por tanto I+ = I- = 0A
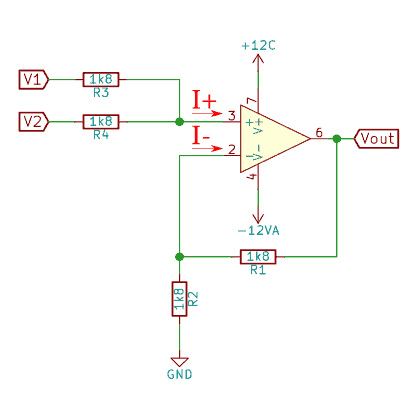
Nuestro primer objetivo para obtener la ecuación del circuito es calcular cuando vale V+ en función de V1 y V2.
Partamos de la premisa que V1 es mayor que V2 (V1 > V2). Como entre V1 y V2 existe una diferencia de potencial y ambos puntos están unidos por medio de dos resistencias en serie, por ellas debe circular una corriente. Desconocemos el valor de esas corrientes, pero si sabemos por donde circulan.
Pensemos en el punto A. En él hay conectadas tres ramas, la primera es la que viene de la resistencia 3, la segunda la que va a la resistencia 4 y cuarta la que va hacia la entrada no inversora del amplificador operacional sumador no inversor. Si tenemos un nodo con tres ramas, podemos aplicar la Ley de Nodos de Kirchhoff o también llamada Ley de corrientes. La suma de todas las corrientes que entran es igual a la suma de todas las corrientes que salen.
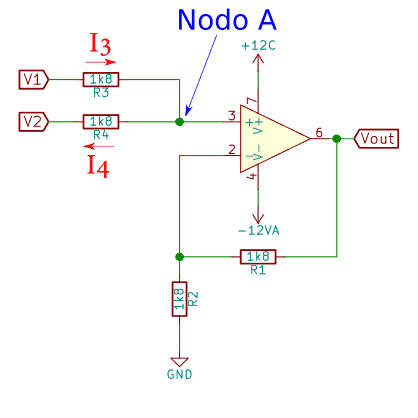
Considera que entra corriente por desde la resistencia R3 y que sale por el resto de ramas, por tanto:
(2) ![]()
Pero como sabemos que la corriente que entra al amplificador es I+ = 0, entonces:
(3) ![]()
Es decir, que la corriente que circula por ambas resistencias es la misma. Para simplificar, a partir de ahora diremos que I3 = I4 = I.
Apliquemos la Ley de Ohm a ambas resistencias:
(4) ![]()
(5) ![]()
En la ecuación (4) se observa como la tensión que cae en la resistencia 3 es la diferencia de tensión entre V1 y V+. En la ecuación (5) ocurre lo mismo para la resistencia 4, sin embargo aplicamos un pequeño truco. La experiencia nos dice que si V1 es mayor que V2, por tanto, V+ tiene que ser mayor que V2. Es por esto último que en la ecuación (5) cambiamos el orden de las tensiones con respecto a la ecuación anterior. En caso de no hacerlo, el circuito se resuelve igual, solo que con un signo negativo.
Como ambas resistencias son iguales, podemos decir que R3 = R4 = R y además ambas corrientes son iguales, podemos igualar las ecuaciones (4) y (5) y despejar V+.
(6) ![]()
Primer objetivo cumplido. Ya tenemos V+ 🙂
Segundo objetivo, buscar una relación entre V+ y Vout. Si te fjas R1 Y R2 forman un divisor de tensión entre Vout y masa (GND), por tanto podemos aplicar la ecuación del divisor de tensión con referencia a GND.
(7) ![]()
Como R1 y R2 son iguales entre sí, R1 = R2 = R, si sustituimos y despejamos Vout:
(8) ![]()
Por tanto, ya tenemos una relación entre Vout y V+. Combinando las ecuaciones (6) y (8) se obtiene la ecuación que venimos usando desde el principio.
(9) ![]()
Como ves, ser trata casi en exclusiva de usar un análisis de nodos y corrientes.
Usos de amplificador sumador de voltaje
El sumador no inversor de tensión o amplificador sumador de voltaje lo podemos usar en gran multitud de circuitos, en realidad en todos aquellos en los que debamos sumar dos tensiones.
Un ejemplo clásico es offset a una señal, tal y como hacemos en este vídeo. Si tenemos una señal cuadrada (o de cualquier tipo) a la que debamos añadirle un offset, lo podemos hacer fácilmente con un sumador de tensión. En la entrada 1 se conectaría la señal cuadrada y en la entrada 2 pondríamos la tensión de offset, la cual puede provenir de un potenciómetro. Eso sí cuidado con los efectos de carga.
Otro uso puede ser eliminar una parte de la señal, por ejemplo, la componente continua de la misma y dejar a la salida del sumador solo la tensión no constante. Este, de hecho, es el último uso que yo le di, restando la componente continua de la señal de un fotodiodo.
También puede ser útil cuando se trata de trabajar con señales diferenciales. Aunque no es la mejor opción para trabajarlas.
Restar con un amplificador sumador, ¿amplificador restador?
¿se puede restar con un amplificador operacional? ¡Claro! Ten en cuenta que una resta no es más que una suma en la que el segundo sumando es negativo. Sin embargo debemos realizar un paso previo, debemos negar la entrada que debe restar.
Supón que quieres restar V1 – V2, esto es lo mismo que sumar V1 + (-V2). Por tanto, primero invertimos el signo de V2 y luego lo sumamos. Un ejemplo es el siguiente:
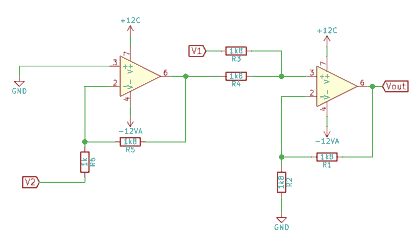
Amplificador sumador inversor
Para terminar vamos a analizar por encima que es un sumador inversor y como se comporta.
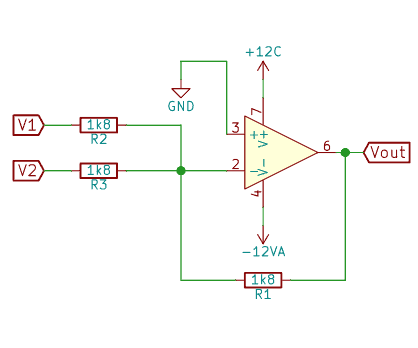
En realidad, un circuito como este lo que hace es sumar y luego cambiar de signo, es decir que la ecuación característica que relaciona la entrada con la salida es:
operacional
(10) ![]()
¿Has usado alguna vez esta configuración del amplificador operacional? ¿Donde la vas a usar el sumador de tensión? Puedes dejar tus dudas y opiniones en los comentarios un poco más abajo.